Descubre cómo midió el matemático griego, Eratóstenes, la Tierra usando tan solo un palo en el solsticio de verano.
El día 21 de junio es el día del solsticio de verano, lo que viene a ser, el día que da comienzo al verano.
Hace más de 2000 años, un matemático llamado Eratóstenes tuvo la grandiosa idea de calcular el radio de la Tierra con tan solo un palo. ¿Que cómo lo hizo? ¡¡Vamos a verlo!!
Procedimiento
- Lo primero que hizo fue conseguir un palo (un paso muy importante si quieres calcular el radio de la Tierra con un palo, valga la redundancia).
- A la hora del mediodía solar en el día del solsticio de verano (todo exacto), puso el palo formando un ángulo de 90 grados con el suelo.
- Midió el ángulo que formaba la punta superior del palo con el extremo de su sombra.
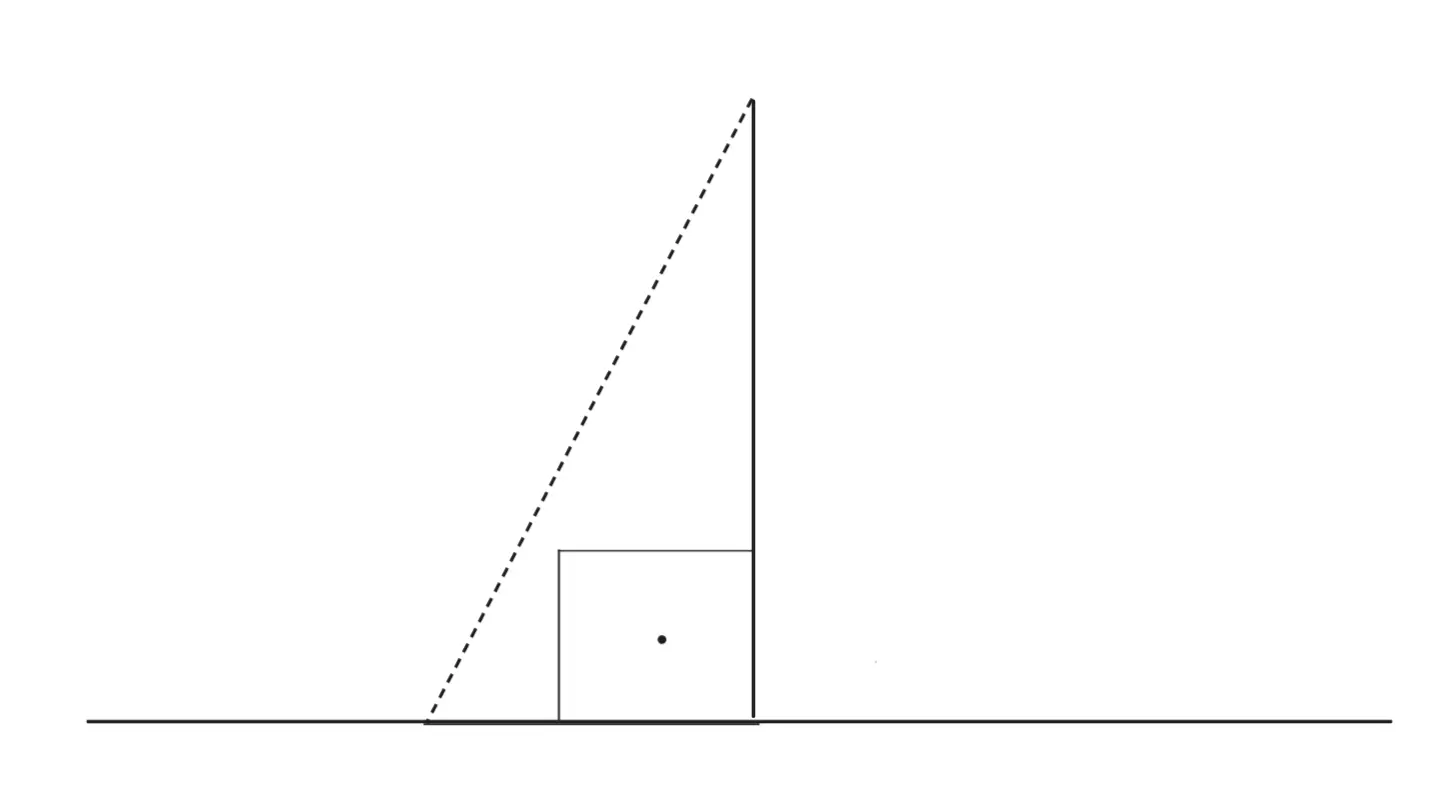4. Una vez tenía lo que medía el ángulo, solo le faltaba una de las cosas más importantes: la distancia desde donde lo hacía (Alejandría) hasta un lugar en el Trópico de Cáncer (él utilizó Siena). Para calcular esta distancia, midió a cuánto equivalía el paso de un esclavo y lo puso a recorrer todo el camino desde Alejandría hasta Siena.
5. Cuando contó con todos los datos, hizo el siguiente cálculo para hallar el radio de la Tierra (importante: la medida del ángulo ha de estar en radianes):
r = distancia/ángulo
Y así fue cómo Eratóstenes descubrió cuánto medía el radio de la Tierra con este simple razonamiento, ¿o no tan simple? ¡¡Veamos la explicación!!
Explicación de cómo midió Eratóstenes la Tierra con un simple palo
Justo a la hora del mediodía solar en el día del solsticio de verano los rayos del Sol caen en el Trópico de Cáncer de forma que ningún objeto tiene sombra.
Si te pones en cualquier lugar justo a esa hora y mides el ángulo que forma el palo que has puesto con la sombra que hace él mismo, podrás observar que, ese ángulo es exactamente el mismo que el que forma el arco desde donde has tomado las medidas hasta el Trópico de Cáncer.
Demostración
Claro, de poco te va a servir decirte todo esto y no hacerte una demostración, ¡pues para eso estamos! Ahora mismo te voy a enseñar paso a paso cómo he replicado yo lo que hizo Eratóstenes hace más de dos mil años.
- El primer paso que hice fue tomar un palo, como no encontraba ninguno, decidí utilizar una botella (ya sabes, hay que reutilizar).
- Esperé a la hora del mediodía solar del 21 de junio de 2022 (14:20) y, cuando llegó la hora, puse en un lugar plano la botella. Medí la longitud de la botella y de la sombra que formaba y los datos eran los siguientes:
- Longitud de la botella = 26 cm.
- Longitud de la sombra = 10 cm.
- Una vez en casa, calculé el arco tangente de estas dos medidas dividiéndose para hallar el ángulo en radianes que formaban:
arctan (10/26) = arctan(0.38) = 0.3631 rad
- Por último, dividí la distancia desde donde lo he heho hasta el Trópico de Cáncer y (siendo la distancia = 2315 km):
r = 2315/0.3631 = 6375 km