El método d’Hondt es una forma de reparto electoral, es decir, un sistema para convertir una cantidad de votos en escaños con el objetivo de hacer un reparto acorde a las peticiones de los votantes tras unas elecciones.
Origen y algunos países que lo usan
Este sistema tiene su origen en 1878 por Víctor d’Hondt, quien fue un jurista belga y profesor de derecho civil y de derecho fiscal en Flandes, concretamente en la Universidad de Gante. Este método se usa en bastantes países del mundo, algunos son: Argentina, Bélgica, Brasil, Croacia, España, Países Bajos y Portugal, entre muchos otros.
Sus características
La principal característica de este método es que beneficia a los partidos grandes frente a los partidos pequeños, lo que muchas veces desemboca en el bipartidismo político. Veremos el caso de las Elecciones Generales del 23J donde proporcionalmente los dos partidos más grandes de España, PP y PSOE deberían tener menos escaños y partidos más pequeños, como SUMAR o VOX deberían tener más escaños a costa de los primeros.
En España
En nuestro país aplicamos este sistema mediante circunscripciones, que son las diferentes provincias. Cada provincia tiene asignados un número de diputados. Como mínimo, la ley establece que cada provincia debe poder elegir a dos diputados, y cada ciudad autónoma (Ceuta y Melilla) elegirá a un diputado cada una. Así, ya estarían asignados 102 escaños y los otros 248 se asignarán de manera proporcional a la población de cada provincia.
La circunscripción con mayor número de escaños es Madrid, con 37 diputados y el resto de circunscripciones tienen los siguientes diputados:
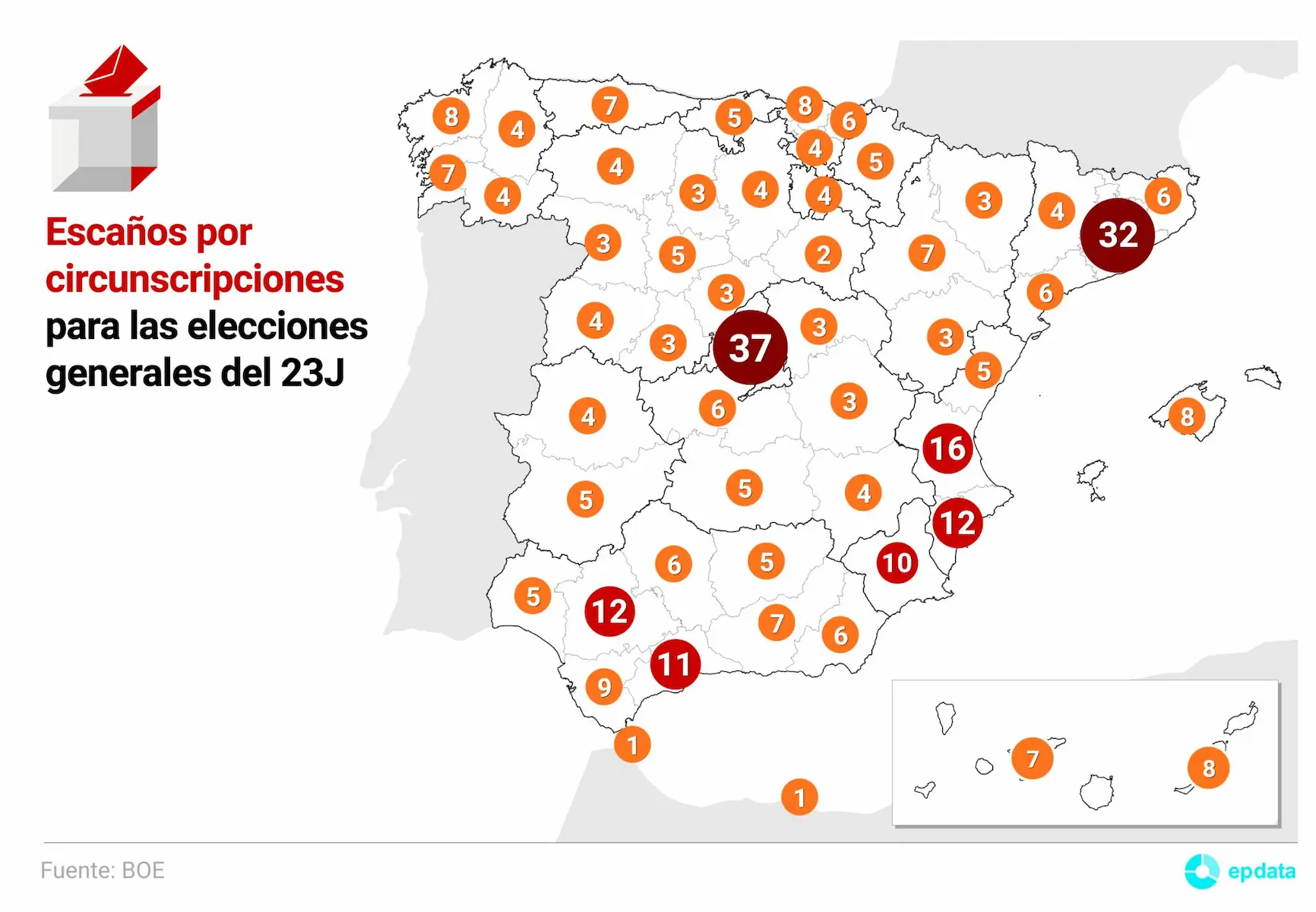
Escaños por circunscripciones para las elecciones generales del 23J. Fuente: BOE. Gráfico: epdata.
Diferencias entre escaños y población
A continuación mostramos una tabla para ver las diferencias que se nos presentan en algunas circunscripciones entre el porcentaje de escaños que se les ha atribuido y el porcentaje de población que tienen, por tanto, el porcentaje de escaños que se les debería atribuir. Está ordenada de menor a mayor diferencia, siendo esta el resultado de restar el porcentaje de escaños menos el porcentaje de población. Por tanto, la circunscripción situada en primer lugar es la que tiene menos escaños de los que debería y la situada en último lugar, la que tiene más escaños de los que debería.
| Circunscripción | % Escaños | % Población | Diferencia (%) |
|---|---|---|---|
| Madrid | 10,57% | 14,07% | -3,50% |
| Barcelona | 9,14% | 12,10% | -2,96% |
| Valencia | 4,57% | 5,49% | -0,92% |
| Sevilla | 3,43% | 4,15% | -0,72% |
| Alicante | 3,43% | 4,00% | -0,57% |
| Málaga | 3,14% | 3,63% | -0,48% |
| Murcia | 2,86% | 3,22% | -0,36% |
| Baleares | 2,29% | 2,57% | -0,29% |
| Santa Cruz de Tenerife | 2,00% | 2,21% | -0,21% |
| Vizcaya | 2,29% | 2,42% | -0,13% |
| Asturias | 2,00% | 2,09% | -0,09% |
| Las Palmas | 2,29% | 2,38% | -0,09% |
| La Coruña | 2,29% | 2,34% | -0,05% |
| Cádiz | 2,57% | 2,62% | -0,05% |
| Zaragoza | 2,00% | 2,04% | -0,04% |
| Tarragona | 1,71% | 1,75% | -0,03% |
| Pontevedra | 2,00% | 1,99% | 0,01% |
| Badajoz | 1,43% | 1,41% | 0,02% |
| Navarra | 1,43% | 1,40% | 0,03% |
| Girona | 1,71% | 1,67% | 0,04% |
| Granada | 2,00% | 1,94% | 0,06% |
| Córdoba | 1,71% | 1,63% | 0,08% |
| Melilla | 0,29% | 0,18% | 0,10% |
| Ceuta | 0,29% | 0,18% | 0,11% |
| Almería | 1,71% | 1,59% | 0,12% |
| Jaén | 1,43% | 1,30% | 0,13% |
| Guipúzcoa | 1,71% | 1,53% | 0,18% |
| Castellón | 1,43% | 1,24% | 0,19% |
| León | 1,14% | 0,94% | 0,20% |
| Cantabria | 1,43% | 1,22% | 0,20% |
| Toledo | 1,71% | 1,49% | 0,22% |
| Lleida | 1,14% | 0,91% | 0,23% |
| Guadalajara | 0,86% | 0,57% | 0,29% |
| Huelva | 1,43% | 1,11% | 0,31% |
| Cáceres | 1,14% | 0,82% | 0,32% |
| Albacete | 1,14% | 0,81% | 0,33% |
| Valladolid | 1,43% | 1,10% | 0,33% |
| Soria | 0,57% | 0,19% | 0,38% |
| Ciudad Real | 1,43% | 1,04% | 0,39% |
| Huesca | 0,86% | 0,47% | 0,39% |
| Burgos | 1,14% | 0,75% | 0,39% |
| Álava | 1,14% | 0,71% | 0,43% |
| Cuenca | 0,86% | 0,41% | 0,44% |
| Salamanca | 1,14% | 0,69% | 0,45% |
| Lugo | 1,14% | 0,67% | 0,47% |
| La Rioja | 1,14% | 0,67% | 0,47% |
| Zamora | 0,86% | 0,36% | 0,50% |
| Ourense | 1,14% | 0,64% | 0,51% |
| Palencia | 0,86% | 0,34% | 0,52% |
| Ávila | 0,86% | 0,33% | 0,53% |
| Segovia | 0,86% | 0,32% | 0,53% |
| Teruel | 0,86% | 0,28% | 0,57% |
Destacan Madrid y Barcelona como circunscripciones que tienen notablemente menos escaños de los que deberían tener según su población: 49 escaños y 42 respectivamente, en vez de 37 y 32. Les siguen provincias como Valencia, Sevilla o Alicante, que también tendrían dos o tres escaños más cada uno.
Por la cola encontramos circunscripciones como Palencia, Ávila, Segovia o Teruel, que tienen dos escaños por ley (lo mínimo), pero proporcionalmente deberían tener uno.
Cómo funciona este método
Ahora veremos cómo funciona realmente este sistema con un ejemplo: vamos a repartir 5 escaños entre cuatro partidos: A, B, C y D. En total hay 100 votos:
- A obtiene 43 votos.
- B obtiene 28 votos.
- C obtiene 15 votos.
- D obtiene 14 votos.
Para transformar estos votos en escaños debemos dividir la cantidad que ha obtenido cada partido entre 1, 2, 3…, así hasta llegar a 5, que es el número de escaños que queremos repartir. Si quisiéramos repartir más escaños, tendríamos que dividir hasta dicho número de escaños. Pondremos los resultados de las divisiones en una tabla:
| Partido | /1 | /2 | /3 | /4 | /5 |
|---|---|---|---|---|---|
| A | 43 | 21,5 | 14,3 | 10,75 | 8,6 |
| B | 28 | 14 | 9,3 | 7 | 5,6 |
| C | 15 | 7,5 | 5 | 3,75 | 3 |
| D | 14 | 7 | 4,7 | 3,5 | 2,8 |
Para ver cuántos escaños tiene cada partido, vemos cuáles son los cinco cocientes más altos después de hacer todas las divisiones:
- A tiene tres de los cocientes más altos, por tanto tiene 3 escaños.
- B tiene uno de los cocientes más altos, por tanto tiene 1 escaño.
- C tiene uno de los cocientes más altos, por tanto tiene 1 escaño.
- D no tiene ninguno de estos cocientes, por tanto no tiene escaños.
Genial, ya sabemos cuántos escaños le corresponderían a cada partido según este método, pero ¿realmente son proporcionales? ¿O estamos beneficiando a los partidos más grandes como comentamos antes? Veamos:
- A tiene un 43% de los votos, lo que se convierte en 2,15 escaños aproximadamente → 2 escaños
- B tiene un 28% de los votos, lo que se convierte en 1,4 escaños aproximadamente → 1 escaño
- C tiene un 15% de los votos, lo que se convierte en 0,75 escaños aproximadamente → 1 escaño
- D tiene un 14% de los votos, lo que se convierte en 0,7 escaños aproximadamente → 1 escaño
En este ejemplo vemos perfectamente cómo el partido más votado ha ganado un escaño más de los que se merecía proporcionalmente a costa de que el partido menos votados haya perdido un escaño que, proporcionalmente, sí merecía tener.
Este método es el que se aplica en cada circunscripción de España, según los votos obtenidos en dicha circunscripción y el número de escaños asignados y, finalmente, se suman los escaños conseguidos en todo el territorio para el resultado final.
¿Y si hubiera una circunscripción única en España?
Muchas veces nos preguntamos: ¿y qué pasaría si todos los votos en España valieran lo mismo independientemente de dónde tengan lugar? En este artículo veremos, con un programa de Python que nos lo calculará, si habría mucha diferencia con los datos de las últimas elecciones generales o no. Este es el fragmento de código:
# Introducir datos sobre escaños y partidos
nEscanos = int(input("Número de escaños: "))
nPartidos = int(input("Número de partidos: "))
# Creación de diccionario para partidos y escaños, y de una lista para los cocientes
partidos = {}
cocientes = []
# Por cada partido
for a in range (nPartidos):
# Introducir nombre del partido y votos
nombre = input("Nombre del partido: ")
votos = int(input("Número de votos: "))
# Poner el contador de escaños a 0
partidos[nombre] = 0
# Por cada escaño, hacer la división y añadirla a la lista de cocientes
for b in range (nEscanos):
cocientes.append([votos/(b+1), nombre])
# Ordenar la lista de cocientes de menor a mayor
cocientes.sort()
# Por cada escaño, coger el último cociente (el mayor), eliminarlo de la lista y sumarle un escaño a dicho partido
for a in range (nEscanos):
partidos[cocientes.pop(0)[1]] += 1
# Imprimir el diccionario con los partidos y los escaños de cada uno
print(partidos)
Resultados
| Partido | Votos | 23J | Circunscripción única | Diferencia |
|---|---|---|---|---|
| PP | 8,091,840 | 137 | 120 | -17 |
| PSOE | 7,760,970 | 121 | 115 | -6 |
| VOX | 3,033,744 | 33 | 45 | +12 |
| SUMAR | 3,014,006 | 31 | 45 | +14 |
| ERC | 462,883 | 7 | 6 | -1 |
| Junts | 392,634 | 7 | 5 | -2 |
| EH Bildu | 333,362 | 6 | 4 | -2 |
| PNV | 275,782 | 5 | 4 | -1 |
| BNG | 152,327 | 1 | 2 | +1 |
| CCa | 114,718 | 1 | 1 | 0 |
| UPN | 51,764 | 1 | 0 | -1 |
| PACMA | 165,768 | 0 | 2 | +2 |
| CUP | 98,794 | 0 | 1 | +1 |
Con una circunscripción única los dos partidos más grandes perderían bastantes diputados, que los ganarían, principalmente VOX y SUMAR. También hay partidos como PACMA o CUP que antes no tenían representación y con una circunscripción única sí tendrían representación. En cambio, otros partidos pequeños pierden representación, como UPN, ya que pierden el factor del voto dentro de la circunscripción que beneficiaba a partidos locales frente a partidos como PACMA que no obtienen muchos votos en una circunscripción, pero sí a lo largo de todo el territorio.
Finalmente, ¿es proporcional?
Para terminar, analizaremos si los escaños que obtuvieron el pasado 23J son proporcionales a los votos recibidos.
| Partido | Votos | 23J | Escaños Proporcionales | Diferencia |
|---|---|---|---|---|
| PP | 8,091,840 | 137 | 131.77 | -5.23 |
| PSOE | 7,760,970 | 121 | 115.82 | -5.18 |
| VOX | 3,033,744 | 33 | 39.32 | +6.32 |
| SUMAR | 3,014,006 | 31 | 38.70 | +7.70 |
| ERC | 462,883 | 7 | 6.87 | -0.13 |
| Junts | 392,634 | 7 | 5.82 | -1.18 |
| EH Bildu | 333,362 | 6 | 4.91 | -1.09 |
| PNV | 275,782 | 5 | 4.20 | -0.80 |
| BNG | 152,327 | 1 | 1.90 | +0.90 |
| CCa | 114,718 | 1 | 1.43 | +0.43 |
| UPN | 51,764 | 1 | 0.64 | -0.36 |
| PACMA | 165,768 | 0 | 2.06 | +2.06 |
| CUP | 98,794 | 0 | 1.22 | +1.22 |
En este último apartado calculamos cuántos escaños le correspondería a cada partido de forma proporcional a los votos recibidos. Hay que tener en cuenta que este no es un resultado muy certero, pues no tenemos en cuenta las diferentes circunscripciones del país y lo hacemos como si fuera una circunscripción única.
Tal y como llevamos comentando todo el artículo, en un reparto proporcional perderían los dos partidos principales, PP y PSOE, y ganarían los partidos medianos, VOX y SUMAR. Al igual que ocurrió haciendo una circunscripción única con el método d’Hondt, partidos como PACMA y CUP obtienen representación al eliminar el factor de beneficio para los partidos locales que otorgaban las diferentes circunscripciones.
Conclusiones finales
En resumen, este método de reparto favorece a los partidos más grandes, dando lugar muchas veces al bipartidismo, y perjudicando a partidos más pequeños. También es importante conocer que en España tenemos diferentes circunscripciones que hacen que los partidos locales cobren importancia por los escaños que puedan obtener en sus localidades, al obtener más votos en una localidad que otros partidos, pero menos en todo el país.


